|
1.3.8.4 Глубина резкости
Термин «глубина резкости» хорошо известен всем, кто хоть раз сталкивался с фотографией или посещал выставки профессиональных фотографов. Умело,
используя глубину резкости, фотографы создают высокохудожественные
снимки, выделяя главный сюжет и сглаживая все, что находится на втором
плане. Такие возможности открылись перед фотографами с появлением на
корпусе объектива шкалы с нанесенными на ней расстояниями глубины
резкости. Для создания такой шкалы была создана методика расчета,
использующая в качестве переменных расстояние наводки на резкость,
диафрагменное число, фокусное расстояние объектива, а так же диаметр
допустимого кружка рассеяния. Из перечисленных параметров только диаметр
допустимого кружка рассеяния для нас является новым, но о нем немного
позже.
В отличие от фотографических объективов, объективы, используемые в
системах видеонаблюдения, не имеют шкалы глубины резкости. Объясняется
это тем, что для объективов, имеющих автоматическую диафрагму, не
существует постоянного значения глубины резкости. В таких объективах она
меняется в зависимости от значения диафрагмы, которая определяется
реальной освещенностью на объекте. Для объективов с ручной диафрагмой
отсутствие шкалы глубины резкости можно объяснить, скорее всего,
невостребованностью этого параметра потребителями систем охранного
телевидения.
Глубиной резкости называется свойство объектива изображать в одной
плоскости и практически с одинаковой резкостью предметы, удаленные от
объектива на различные расстояния.
Рассмотрим, что такое глубина резкости при формирования изображения на
ПЗС матрице видеокамеры. Назовем пространство перед объективом –
«Предметное пространство», а пространство между объективом и
видеокамерой – «Пространство изображений». Пусть у нас имеется три
точечных источника изображения «B», «C» и «D» (рис. 18), находящихся на
разном удалении от видеокамеры.
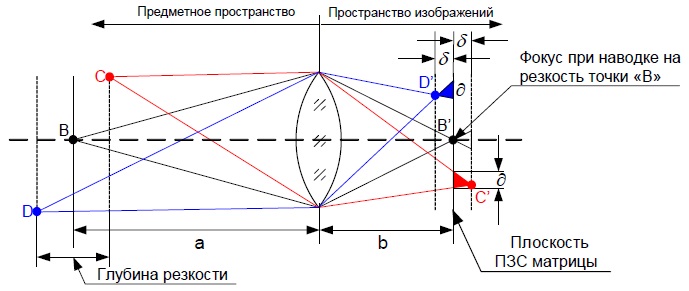
Рис. 18 - Определение глубины резкости
Наведем резкость объектива на точку «В». Объектив сфокусирует ее в точке
«В’» на ПЗС матрице. Монитор, подключенный к видеокамере, сформирует
резкое изображение точечного источника. Точки «С» и «D», лежащие в
других плоскостях так же сфокусируются в точках «С’» и «D’», а на ПЗС
матрице создадут не точки, а кружки диаметром ∂.
Монитор тоже отобразит их на экране. В зависимости от того, на сколько
точки «D» и «C» отстоят от точки наводки на резкость «B», кружки будут
иметь разный диаметр. Из этих построений следует, что оптическая
система, формируя изображение, не имеет ни какой глубины резкости.
Резкими будут только те точки, которые лежат в плоскости наводки на
резкость. Это подтверждает и основное уравнение линзы.
Но из практики мы хорошо знаем, что глубина резкости существует и более
того ею можно управлять, выбирая нужный диапазон в зависимости от
поставленных задач. Так чем же определяется глубина резкости и от чего
она зависит? На самом деле глубина резкости это следствие ограниченных
возможностей человеческого зрения. Если напечатать на листе бумаги
кружки с разным диаметром но меньше 0,1 мм и рассматривать их
невооруженным глазом с расстояния наилучшего зрения (25 см), то нам
будет казаться, что все они одного размера. Другими словами человеческий
глаз не в состоянии различить ни размеры кружка, ни тем более их
содержание, если диаметр кружка равен или меньше 0,1 мм.
Допустим, что отображаемый на мониторе кружок ∂
(рис.18), который передает изображение точек «C» или «D», имеет на
мониторе такой размер, что глаз не в состоянии отличить его от точки
«B». Тогда точки D’ и B’ сфокусированные рядом с ПЗС матрицей, на
мониторе будут тоже резкими, потому, что мы видим их не как кружек, а
как точку. Следовательно, и в предметном пространстве точки D, B и все
предметы между ними будут резкими, а расстояние между плоскостями D и C
будет называется глубиной резкости. Параметр «∂»
в профессиональной терминологии называется кружком рассеяния. Наша
задача состоит в том, чтобы связать размер кружка рассеяния с
характеристиками человеческого зрения в зависимости от диагоналей
мониторов и расстояний, с которых оператор анализирует изображение. В
дальнейшем размер этого кружка будет использоваться для расчета глубины
резкости и гиперфокального расстояния, а сам кружек будет называться
допустимым кружком рассеяния.
Используя фотографическую методологию в обосновании диаметров допустимых
кружков рассеяния, выберем размеры допустимых кружков рассеяния и для
систем охранного телевидения.
Из чего исходили классики в фотографии? Прежде всего, они выбрали
критерий и, руководствуясь им, проводили все расчеты. Критерий самый
банальный - это разрешающая способность человеческого глаза или свойство
человеческого зрения видеть мелкие предметы на изображении. И
действительно, человеческое зрение имеет конечные возможности, которые
определяются минимальным углом α (рис. 19),
под которым глаз способен различать мелкие детали на изображении. В
зависимости от удаления предмета рассматривания, линейные размеры
нечувствительности глаза увеличиваются. Для среднестатистического
человека глаз в состоянии различать мелкие детали с углом зрения не
менее 0,017 градусов, что соответствует диаметру кружка рассеяния 0,074
мм на расстоянии рассматривания 25 см. В то же время на расстоянии в
один метр диаметр кружка будет уже 0,3 мм. Зная предельный угол зрения
глаза и, задавшись расстоянием просмотра можно построить таблицу
минимальных кружков рассеяния.
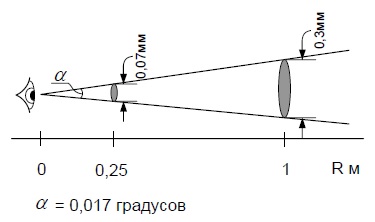
Рис. 19 - Определение минимального угла зрения
В фотографии [15] размеры кружков рассеяния были определены как раз
таким способом (Таблица 3).
Таблица 3 - Размеры кружков рассеяния
| Предмет рассматривания |
Расстояние просматривания, м |
Диаметр кружка рассеяния, мм |
| Теоретический |
Практический |
| Негатив |
0,1 |
0,03 |
0,04 |
| 0,15 |
0,04 |
0,06 |
| 0,2 |
0,06 |
0,08 |
| Фотография |
0,25 |
0,07 |
0,1 |
| 0,3 |
0,09 |
0,12 |
| 0,4 |
0,12 |
0,16 |
| Выставочные фотографии |
0,5 |
0,15 |
0,2 |
| 0,75 |
0,22 |
0,3 |
| 1 |
0,29 |
0,4 |
| 1,5 |
0,44 |
0,6 |
Однако предельный угол зрения человек не всегда способен или хочет
реализовать, тем более что у каждого человека зрение абсолютно
индивидуально. Наверно поэтому, а может быть и из многолетнего опыта
работы, размеры кружков рассеяния в фотографии приняли в 1,33 раза
больше чем теоретически обоснованные. Такой размер кружков соответствует
углу зрения глаза 0,023 градуса. В таблице 3 это столбец «Практический».
Нетрудно заметить, что самый маленький кружок рассеяния относится к
негативу при минимальном расстоянии просмотра. И это вполне естественно,
так как при увеличении негатива до размеров даже среднего формата
фотографии, кружок рассеяния так же увеличится пропорционально
выбранному масштабу и может превысить свое допустимое значение. В
результате чего расчетная глубина резкости не будет соответствовать ее
действительному значению. Хочется обратить внимание читателей, что в
фотографии при обосновании параметра допустимого кружка рассеяния ни
какие технические характеристики объективов, фотопленок или фотокамер не
использовались.
Если подходить к выбору кружка рассеяния, для охранного телевидения
используя опыт фотографии, то правильней было бы пересчитать размер
кружка рассеяния на мониторе к его размеру на ПЗС матрице. Кружок
рассеяния на мониторе можно выбрать, руководствуясь предельным
разрешением человеческого зрения в зависимости от удаления оператора от
монитора. Но однозначно определить с какого расстояния оператор будет
смотреть на монитор, а тем более значение диагонали монитора предвидеть
достаточно трудно. Тем не менее, удаление оператора от монитора, при
проектировании рабочего места регламентируется медицинскими
ограничениями (Таблица 4), которые составляют величину порядка 4-х
диагоналей экрана.
Таблица 4 - Медицинские ограничения удаления оператора от монитора
при проектировании рабочего места.
| Диагональ монитора |
Рекомендуемое расстояние (м) |
| Медицинские ограничения |
Наилучший просмотр |
| 9" |
0,91 |
0,5 |
| 12" |
1,22 |
0,7 |
| 14" |
1,42 |
0,8 |
| 17" |
1,73 |
1 |
| 21" |
2,13 |
1,2 |
Для детального изучения изображения оператор обычно смотреть на монитор
с минимальных расстояний и использует для этих целей специальные
просмотровые мониторы, имеющие увеличенную диагональ экрана. Но смотреть
на монитор 21” с очень близкого расстояния не имеет смысла, так как
оператор в этом случае видит не картинку, а структуру кинескопа. Поэтому
для просмотровых мониторов существуют расстояния наилучшего просмотра
картинки. Эти расстояния получены на основе свойства человеческого
зрения, видеть изображение с высоким разрешением при минимальном
зрительном напряжении. Это возможно только с расстояний, при которых
угол зрения глаза находится в пределах 20 градусов. В таблице 4 эти
расстояния сведены в столбец «Наилучший просмотр». На основании этих
рассуждений получены значения кружков рассеяния (Таблица 4) для
расстояний наилучшего просмотра (верхняя строка) и расстояний,
нормируемых медицинскими ограничениями (нижняя строка). В расчетах
использовался угол зрения глаза равный 0,017 градусов.
В качестве допустимых кружков рассеяния для различных форматов ПЗС
матриц (Таблица 5) можно использовать усредненные значения по наилучшему
просмотру.
В связи с тем, что это расчетные значения, а практика, как правило,
вносит свои коррективы, то вполне возможно, что кружки рассеяния могут
быть большего размера, хотя бы как в фотографии в 1,33 раза.
Определив допустимые размеры кружков рассеяния можно попробовать
рассчитать глубину резкости и гиперфокальные расстояния.
Найдем глубину резкости для видеокамеры с форматом матрицы 1/3”,
диафрагменным числом 1,3 и фокусными расстояниями в диапазоне от 2,8 до
16 мм. Сфокусируем объектив на условный предмет, расположенный на
удалении от камеры 10 м.
Таблица 5 - Кружки рассеяния для различных форматов ПЗС матриц
| Диагональ монитора
(дюйм) |
Расстояние
просматривания, (м) |
Диаметр кружка рассеяния на ПЗС
матрице, мкм |
| Формат кристалла матрицы |
| 1/4 |
1/3 |
1/2 |
2/3 |
| 9 |
0,5 |
2,8 |
3,9 |
5,2 |
7,1 |
| 0,91 |
5,0 |
7,1 |
9,4 |
12,0 |
| 12 |
0,7 |
2,9 |
4,1 |
5,4 |
7,5 |
| 1,22 |
5,0 |
4,0 |
9,2 |
13,0 |
| 14 |
0,8 |
2,8 |
4,0 |
5,3 |
7,3 |
| 1,42 |
5,0 |
7,1 |
9,5 |
13,0 |
| 17 |
1 |
2,9 |
4,1 |
5,5 |
7,6 |
| 1,73 |
5,0 |
7,0 |
9,5 |
13,0 |
| 21 |
1,2 |
2,8 |
4,0 |
5,3 |
7,0 |
| 2,13 |
5,0 |
7,0 |
9,5 |
13,0 |
|
Усредненные значения по: |
|
|
|
|
|
наилучшему просмотру |
2,8 |
4,0 |
5,3 |
7,3 |
|
медицинским ограничениям |
5,0 |
6,4 |
9,4 |
12,8 |
Таблица 6 - Зависимость фокусного расстояния объектива от глубины
резкости
| Глубина резкости |
Фокусные расстояния, мм |
|
2,8 |
4 |
6 |
8 |
12 |
16 |
|
Минимальное расстояние (м) |
1,3 |
2,3 |
4,0 |
5,4 |
7,3 |
8,3 |
|
Максимальное расстояние (м) |
∞ |
∞ |
∞ |
61,0 |
16,0 |
13,0 |
Резкость наводилась на объект, удаленный на 10 м.
Из результатов расчетов (таблица 6) видно как с увеличением фокусного
расстояния объектива глубина резкости уменьшается, сходясь на расстоянии
наводки на резкость 10 м. Поскольку в нашем примере диафрагма полностью
открыта, то эти данные справедливы для вечернего времени, когда
освещенность мала или днем, но в том случае, когда используются
видеокамеры с автоматическим затвором и бездиафрагменным объективом.
Таблица 7 - Значения глубины резкости в зависимости от значения
диафрагменного числа
| Глубина резкости |
Фокусные расстояния, мм |
|
2,8 |
4 |
6 |
8 |
12 |
16 |
|
Минимальное расстояние (м) |
0,23 |
0,46 |
0,98 |
1,6 |
3,0 |
4,4 |
|
Максимальное расстояние (м) |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
В дневное время, когда диафрагма закрывается, глубина резкости
значительно увеличивается. В таблице 7, для этих условий приведены
значения глубины резкости при диафрагменном числе 8.
Объясним увеличение глубины резкости в зависимости от значения
диафрагменного числа (Рис. 20).
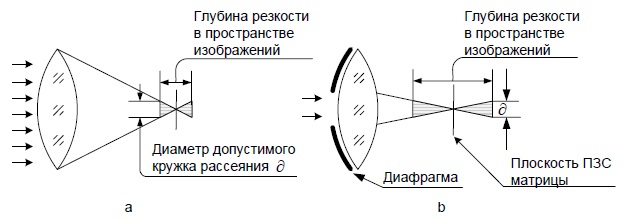
Рис. 20 - Зависимость глубины резкости от значения диафрагменного числа
Если диафрагма полностью открыта (Рис. 20а), то все лучи сходятся в
фокусе на ПЗС матрице. Зная диаметр допустимого кружка рассеяния ????
можно определить глубину резкости относительно плоскости ПЗС матрицы.
Если мы закроем объектив диафрагмой (Рис. 20б), то лучи сойдутся в той
же точке фокуса, но допустимый кружок рассеяния будет отстоять от
плоскости ПЗС матрицы значительно дальше и как следствие глубина
резкости будет больше.
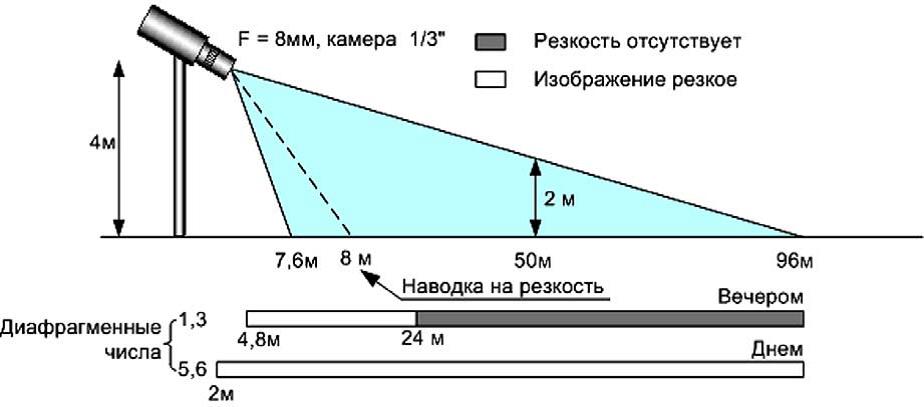
Рис. 21 - Зависимость глубины резкости в дневное и вечернее время от
расстояния наводки на резкость объектива с автоматической диафрагмой
Рассмотрим пример, как изменится глубина резкости в дневное и вечернее
время в зависимости от расстояния наводки на резкость объектива с
автоматической диафрагмой. На рис. 21 изображена видеокамера,
установленная на высоте 4 м с форматом кристалла 1/3” и фокусным
расстоянием объектива 8 мм. Сектор, который способна видеть видеокамера
простирается от 7,6 м до 96 м при угле ее наклона относительно горизонта
15 градусов. Предположим, что сектор наблюдения, интересующий службу
безопасности, расположен от 8 м до 50 м. Наведем резкость объектива на
расстояние 8 метров.
В вечернее время, когда диафрагма полностью открыта (диафрагменное число
1,3) резко изображаемое пространство на мониторе будет составлять
величину от 4,8 до 24 метров.
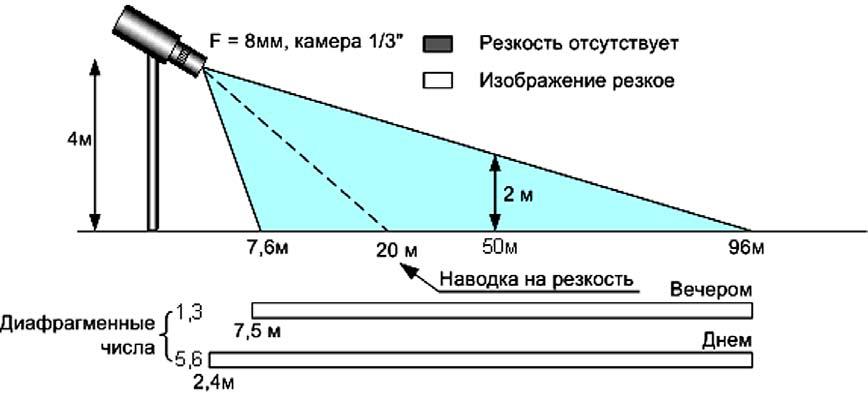
Рис. 22 - Зависимость глубины резкости в дневное и вечернее время от
расстояния наводки на резкость с 8 метров на 20 метров
Это значит, что территория с 24 метров и до 50 метров в вечернее время
суток будет выводиться на монитор нерезкой. С увеличением освещенности
на объекте глубина резкости значительно увеличивается и, будет иметь
значения от 2,0м и до бесконечности. Попробуем изменить расстояние
наводки на резкость с 8 метров на 20 метров (Рис. 22). Глубина резкости
в вечернее время существенно изменилась. Если разместить видеокамеру на
удалении от объектов, которые должны быть под постоянным контролем, не
ближе 7,5 метров мы получим результат, при котором и днем и вечером все
охраняемое пространство будет резким.
Этот пример хорошо показывает насколько важно правильно выбрать
расстояние наводки на резкость.
Оперативно проводить такую оценку можно, имея под рукой
специализированный программный продукт или калькулятор с аналогичными
возможностями. В настоящее время такие задачи может решать
«Проектировщик CCTV», который доступен для приобретения на сайте http://www.lonacomputerservices.com/CCTV/CCTVrus.html
Хочу обратить внимание читателей, что все расстояния, о которых шла речь
в этой статье, будут соответствовать действительности только при условии
правильной настройке «обратного фокуса» объектива.
Знать значения допустимых кружков рассеяния необходимо для того, чтобы
самому рассчитать глубину резкости или гиперфокальное расстояние
объектива.
Значения диаметров допустимых кружков рассеяния в микронах приведены в
таблице 8.
Таблица 8 - Значения диаметров допустимых кружков рассеяния в
микронах
| Формат кристалла матрицы |
| 1/4" |
1/3" |
1/2" |
2/3" |
| 5 |
6,4 |
9,4 |
12,8 |
Глубину резкости можно изменять, варьируя следующими параметрами:
– значение диафрагмы – чем больше диафрагменное число, тем больше
глубина резкости;
– фокусное расстояние – чем больше фокусное расстояние вашего объектива,
тем меньше глубина резкости при фиксированном расстоянии до объекта и
значении диафрагмы. При увеличении фокусного расстояния область резкости
уменьшается из-за увеличения масштаба изображения, что становится
особенно заметно в случае с мощными телеобъективами;
– расстояние от камеры до точки фокусировки – чем ближе вы находитесь к
объекту, тем меньше глубина резкости при одной и той же диафрагме и
неизменном фокусном расстоянии объектива.
Далее
>>> |




