5.2. Количественные критерии оценки

Количественные критерии оценки эффективности программных средств анализа видеоизображений основаны на проведении натурных испытаний по проверке эффективности алгоритма.

Например, проверка детектора движения требует многократного нарушения охраняемой зоны с последующей регистрацией результатов опытов (количество зарегистрированных нарушений и количество пропущенных нарушений).

На основании данных опытов производится вычисление вероятности правильного функционирования алгоритма, (в приведенном далее примере вероятность обнаружения (Р обн.)).

Данные оценки могут базироваться на стандартных «гостированных» методиках оценки, например, на методике, описанной в стандарте СТ СЭВ 5313-85 «Прикладная статистика. Правила определения доверительных границ для биноминального и отрицательно биноминального распределения».

Однако, данные методики сложны для понимания, трудны в практической реализации. В первую очередь эти методики требуют проведения большого количества опытов (обычно количество опытов должно превышать 100 испытаний). В некоторых испытаниях данный подход неприемлем (например, регистрация дыма и пламени с помощью алгоритмов видеоаналитики).

Поэтому ниже проводится упрощенная методика количественной оценки правильности функционирования алгоритма видеоаналитики, взятой из книги Е.С. Вентцель «Теория вероятностей» издательство «Наука» 1969 г.

Данная методика более проста для понимания и реализации.

В основе данной методики лежит понимание, что с уменьшением количества проведенных испытаний мы получаем вероятность события, находящегося в некотором доверительном интервале, т.е. в диапазоне возможных ошибок (для получения более строгого математического определения доверительного интервала следует обратиться к Е.С. Вентцель «Теория вероятностей»).

Рассмотрим на примере расчет вероятности события.

Провели 5 опытов, из них обнаружили вторжение в 4 случаях, Р_обн=4/5=0,8.

Примечание. Вероятность события

А(Р(А))=m/n

где m - число появлений А; n - общее число произведенных опытов.

Поэтому А(Р(А))=4/5=0,8

Далее нам надо определить доверительный интервал для этой вероятности.

Примечание. Доверительный интервал - интервал значений параметра, совместимых с опытными данными и не противоречащих им.

Обращаемся к графику по определению доверительного интервала, взятого из Е.С. Вентцель «Теория вероятностей» издательство «Наука» 1969 г., рис 14.5.2 Вид графика приведен ниже.

На этом графике по вертикали отложены значения доверительного интервала, по горизонтали - вероятность события наших опытов. Цифра над линиями графиков указывает на количество проведенных опытов (в данном случае - 5 опытов).

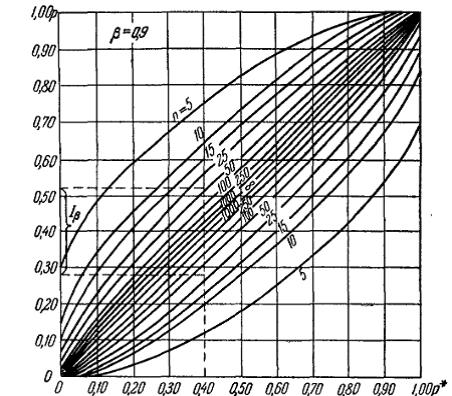
Рис. 18 - График по определению доверительного интервала

На данном графике показано, что вероятность обнаружения Р_обн=0,8 (т.е. провели пять опытов, из них положительными оказались четыре. Р_обн=4/5=0,8). При этом величина доверительного интервала составила величину от 0,42 до 0,97 с вероятностью β=0,9.

Значение по количеству опытов уменьшать нельзя, поскольку границы доверительного интервала уже достаточно большие.

Результаты положительных опытов уменьшить нежелательно. Снижение этих результатов даже на одно значение, (т.е. провели пять опытов, из них положительными оказались три. Р_обн=3/5=0,6), дает Р_обн=0,6, (хотя данный результат может быть приемлем при сложных условиях эксплуатации или при многорубежной охране).

Увеличение количества опытов уменьшает ширину доверительного интервала, что является положительным фактором.

Примечание.

В некоторых случаях возможно проведение опытов в количестве 100 и более раз (например, определение номеров проезжающих машин). Тогда доверительный интервал для вероятности обнаружения Р_обн=0,8 будет всего в пределах от 0,74 до 0,82.

Иногда бывают случаи, когда в 10 опытах получили 10 обнаружений, однако это не значит, что вероятность обнаружения = 1, тогда надо использовать другую формулу.

При этом производят расчет вероятности, исходя из того, что событие не произошло, т.е. не обнаружили (см. ниже).

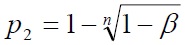
где β - достаточно большая доверительная вероятность (в нашем примере β=0,9),
n - количество опытов.

При пяти положительных опытах (n=5) имеем 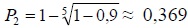, что означает, что вероятность необнаружения составляет 0,369, т.е. вероятность обнаружения 1-0,369=0,631.

Округляя, получим, что система будет обнаруживать 6 человек из 10 с вероятностью 0,9.

При n=10, верхняя граница доверительного интервала 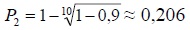, что означает, что вероятность необнаружения составляет 0,206, т.е. вероятность обнаружения 1-0,206=0,794.

Округляя, получим, что система будет обнаруживать 8 человек из 10 с вероятностью 0,9.

При n=25, верхняя граница доверительного интервала 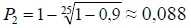, что означает, что вероятность необнаружения составляет 0,088, т.е. вероятность обнаружения 1-0,088=0,912.

Округляя, получим, что система будет обнаруживать 9 человек из 10 с вероятностью 0,9.

Обобщим приведенные выше расчеты для различного количества опытов (5, 10, 25 опытов)

А) n - количество опытов, Р - вероятность обнаружения, I_β - доверительный интервал.

n=5, Р_обн.=0,8, I_β = {0,42-0,97};

n=10, Р_обн.=0,8, I_β = {0,56-0,96};

n=25, Р_обн.=0,8, I_β = {0,67-0,9}.

Б) для случая, когда имели только положительный результат

n=5, Р_обн.=0,6 с вероятностью 90%;

n=10, Р_обн.=0,8 с вероятностью 90%;

n=25, Р_обн.=0,9 с вероятностью 90%.

Среднее время между ложными тревогами (Т_{лож. трев.})

Данный параметр является взаимосвязанным параметром с вероятностью обнаружения (Р_обн.). Чем выше (Р_обн.), тем меньше (Т_{лож. трев.}).

Большое количество ложных тревог негативно сказывается на эффективности охраны, поскольку оператор перестает реагировать на происходящие события, считая их ложной тревогой, поэтому в зависимости от важности охраняемого объекта и значения регистрируемого параметра необходимо разумно выбирать данный параметр.

Из практики обычно считают, что среднее время между ложными тревогами должно быть не более 24 часов.

В общем случае допустимое время между ложными тревогами определяется требованиями заказчика, который определяет их, исходя из специфики несения службы личным составом и важности объекта охраны.

Вывод

Опытным путем, получив приемлемую вероятность Р_обн, не изменяя условий испытаний нужно убедиться в допустимом интервале времени между ложными тревогами.

Часто при проведении приемо-сдаточных испытаний вероятность обнаружения регистрируется при одних настройках системы, а время между ложными тревогами - при других настройках. Данный подход является недопустимым.

Примечание. Иногда Т_{лож. трев.} заменяют вероятностью ложной тревоги. (Р_лт). В нашем случае Т_{лож. трев.} интуитивно более понятно.

Вероятность ложной тревоги. Р_лт - вероятность того, что за время Т произойдет ложное срабатывание системы. Статистически оценивается частота ложных тревог - количество ложных тревог за определенный интервал времени. Средний интервал времени между двумя последовательными ложными срабатываниями называется наработкой на ложное срабатывание (Т_{лож.трев.}). В представлении о пуассоновском характере потока ложных тревог можно записать:

Р_лт = exp^{(Тp./T лож. трев.)}

где: Р_лт. - вероятность ложной тревоги;

Тp.- время нахождения системы в работоспособном состоянии.

Рассмотренные характеристики связаны между собой таким параметром, как чувствительность системы. Чувствительность - величина, обратная порогу. Порог - некое значение, ниже которого воздействие интерпретируется как шумы. Порог регулируется во время настройки системы. Чем больше чувствительность, тем больше вероятность P_обн., но при увеличении чувствительности возрастает и частота ложных тревог (Р_лт.). Эта ситуация показана на рис.19.

При настройке системы приходится лавировать между этими параметрами, при этом задача заключается в подборе оптимального уровня чувствительности.

Часто в научной литературе можно встретить термин «Ошибка первого рода» и «Ошибка второго рода». Данные термины близки по своей сути (Р_обн. и Р_лт).

Ошибки первого рода (англ. type I errors, α errors, false positives) и ошибки второго рода (англ. type II errors, β errors, false negatives) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.

Ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием.

Ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием.

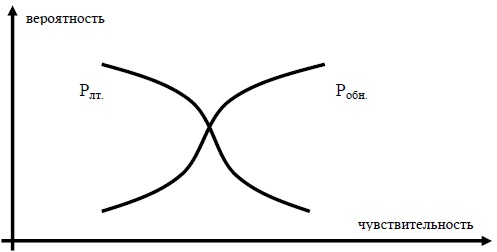
Рис. 19 - Взаимосвязь вероятности обнаружения (Р_обн.) и вероятности ложных тревог Р_лт.

Далее >>>