|
1.3 Зависимость прохождения извещения от соотношения сигнал/шум
Параметр сигнал/шум является наиважнейшим параметром при работе любой
РСПИ. Например, такие важные радиотехнические параметры приемника как
чувствительность, избирательность, стабильность частоты и т.д. служат
одной единственной цели - получению приемлемого соотношения сигнал/шум
на входе решающего устройства (микропроцессора) о принятом бите
информации.
Таблица 1 - Вероятность поражения бита информации в зависимости от
соотношения сигнал/шум
| Uс/Uш |
0,5 |
1 |
1,5 |
2 |
3 |
4 |
5 |
6 |
| Рпор. бита |
0,308 |
0,159 |
0,06 |
0,023 |
1,35х10-3 |
3,17х10-5 |
2,9х10-7 |
10-9 |
Анализ данной таблицы показывает, что при соотношении Uс/Uш=1,5
вероятность поражения (Рпор. бита)=0,06, т.е. из каждых 100 бит
информации поражается 6 бит информации. Для многих систем кодирования
это значение пораженных битов уже является критическим.
Обратите внимание, как быстро уменьшается вероятность поражения бита
информации при росте соотношения сигнал/шум (Uс/Uш).
Примечание. Величина Uс/Uш - безразмерная величина.
При Uс/Uш=2, Рпор. бита=0,023, увеличение в 2 раза Uс/Uш=4, приводит
к Рпор. бита=3,17х10-5 в радиотехнике Uс/Uш=4 принимают за точку
устойчивой работы радиосредств (в том числе и РСПИ). Часто РСПИ
развертываются и работают при Uс/Uш=1,5-2 и пользователи выносят стойкое
убеждение, что РСПИ технически несовершенна или недоведенная, так вот,
при таких Uс/Uш любая РСПИ будет работать неустойчиво. Однако, если Вам
удастся поднять Uс/Uш >5-6, то непрохождение сигнала практически не
будет, например, при Uс/Uш=6, Рпор. бита=10-9, т.е. поражается 1 бит
из миллиарда переданных.
Если Вы не получили соотношение Uс/Uш
≥ 4 (в дБ -12 дБ) на входе
приемника, то РСПИ не будет работать устойчиво, поэтому так важно
измерять при развертывании этот параметр. Отдельные методы измерения Uс/Uш
приведены в Приложении А.
Резкое падение вероятности поражения бита информации при увеличении Uс/Uш
объясняется тем, что распределение отдельных выбросов шума подчиняется
«нормальному» закону распределения вероятностей (см. Рис. 3). При 1,5
σ
вероятность превышения математического ожидания (среднее значение),
определяется площадью, отмеченной на верхнем рисунке красным цветом,
однако при 3 σ, и 6 σ она стремится к нулю, аналогичную зависимость мы
видим и в Таблице 1.
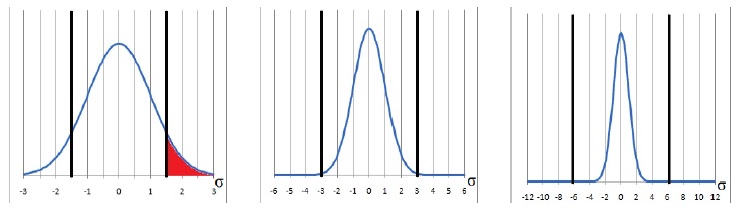
Рис. 3
Вероятность превышение шумом 1,5 σ, 3 σ,
и 6 σ
Примечание. Нормальное распределение функции
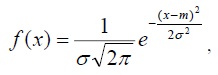
где параметр m - математическое ожидание (среднее значение), а параметр
σ - среднеквадратическое отклонение (σ2 - дисперсия) распределения.
Стандартным нормальным распределением называется нормальное
распределение с математическим ожиданием
µ=0 и стандартным отклонением
σ=1.
Далее
>>> |